Topic Modeling with Non-Negative Matrix Factorization
Unstructured text data provides a wealth of information, but require time and resources to parse through the corpus. As the corpus increases in volume, the energy and resource investment greatly increases as well. Luckily with Topic Modeling, we are able to utilize Statistics and Linear Algebra to quickly and efficiently extract insights. This creates a framework and structure to analyze data in the future, and defined dimensions which allow for clearer communication.
There are a multitude of ways to implement Topic Modeling. Depending on your dataset and the problem statement, different methods would fare better.
A probabilistic approach to this is Latent Dirichlet Allocation (LDA). Another well known way to reduce dimensions is Principal Component Analysis (PCA). Note: when applied to text data, this method is usually referenced as Latent Sentiment Analysis (LSA). I found that Non-Negative Matrix Factorization provided better results than LDA, and LSA.
What is Non-Negative Matrix Factorization (NMF)?
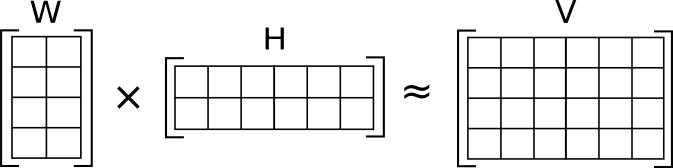
NMF decomposes the original matrix into different components, similar to how LSA is applied. Via matrix factorization, we get 2 matrices: a weight matrix W, and a component matrix H. You can think of each resulting component as a topic.
How does it compare to LSA?
Both are a forms of decomposition, but are implemented with different constraints on the factorization. LSA strives to identify components which are able to capture the greatest variance in the data points. NMF restricts the loading scores of matrices to be strictly non-negative. Philosophically, NMF mirrors the process of text generation more closely aligned with our mental model, as each component adds (non-negative) contributions to the final product.
How do I evaluate the quality of my topics?
Because we are using NMF, we are able to evaluate how well this is able to represent the original matrix. Using the Frobenius norm (aka the Euclidean distance) we can quantify the reconstruction error at different numbers of components/topics. By looking at the gradient of the reconstruction error, we can identify when the gradient seems to be making marginal impact. This is effectively the elbow plot.
What value does Topic Modeling provide?
Topic modeling is able to create structure from an unstructured dataset. In addition to uncovering topics in the data for product development and user/product research, we can utilize these dimensions to compare data and surface recommendations for similar text.
This is a good start to this problem, and by continue to iterate and incorperate feedback into the system, Topic Modeling can provide more product value.